Energy Surface

Plot potential energy surfaces and calculate freqencies for symmetric triatomics

---

source

parse_out

 parse_out (file)

parses an out file of a symmetric triatomic for the bond length, angle and SCF energy

h2o_vals = {}
for filename in os.listdir(h2opath):
    output = parse_out(os.path.join(h2opath, filename))
    h2o_vals[output[0]] = output[1]

---

source

surface_plot

 surface_plot (dict, fname=None)

Plots a surface from the output of the regex

surface_plot(h2s_vals)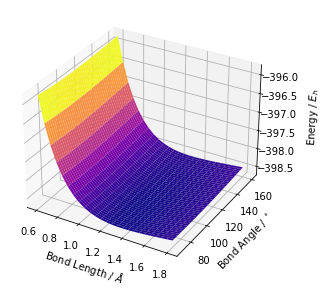

---

source

heatmap

 heatmap (dict, fname=None)

Plots a heatmap from the output of the regex

heatmap(h2o_vals)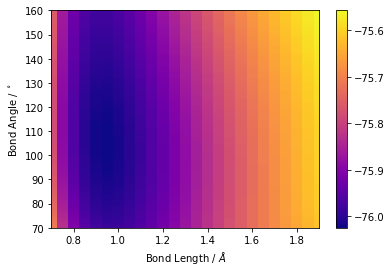

---

source

vib_calc

 vib_calc (dict, mass=1.6735575e-27, plot=False)

Calculate optimum bond length and angle and symmetric stretch and bending frequencies. Default mass is that of the hydrogen atom

Assuming around the equilibrium point, the relevant part of each polynomial is the quadratic, for the stretching frequency: \[E=E_{0}+\frac{1}{2}k_{r}(r-\bar{r})^{2}+\frac{1}{2}k_{\theta}(\theta-\bar{\theta})^{2}\] and thus \[F = -\nabla E=\begin{pmatrix}-k_{r}r\\-k_{\theta}\theta \end{pmatrix}\] and so \(\nu_{r} = \frac{1}{2\pi}\sqrt{\frac{k_{r}}{\mu_{1}}}\) and \(\nu_{\theta} = \frac{1}{2\pi}\sqrt{\frac{k_{\theta}}{r^{2}\mu_{2}}}\), where \(\mu_{1}\approx 2 m_{u}\) and \(\mu_{2}\approx 0.5 m_{u}\). For both water and hydrogen disulfide \(m_{u}\) is the mass of the hydrogen atom

r_opt, theta_opt, nu_r, nu_theta = vib_calc(h2o_vals, plot= True)
print('the optimum bond length of water is ', r_opt, ' angstroms with angle ', theta_opt, ' degrees' )
print('the stretching frequency ', round(nu_r), ' cm-1 and bending frequency ', round(nu_theta), ' cm-1' )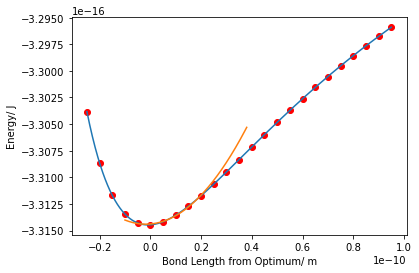

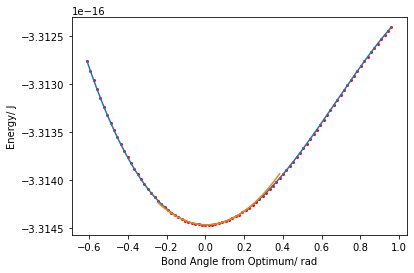
the optimum bond length of water is  0.95  angstroms with angle  105.0  degrees
the stretching frequency  3113  cm-1 and bending frequency  1665  cm-1

Similarly for hydrogen sulfide

r_opt, theta_opt, nu_r, nu_theta = vib_calc(h2s_vals, plot= True)
print('the optimum bond length of hydrogen sulfide is ', r_opt, ' angstroms with angle ', theta_opt, ' degrees' )
print('the stretching frequency ', round(nu_r), ' cm-1 and bending frequency ', round(nu_theta), ' cm-1' )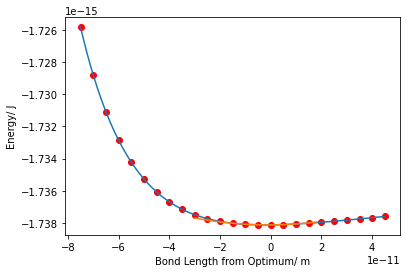

the optimum bond length of hydrogen sulfide is  1.35  angstroms with angle  94.0  degrees
the stretching frequency  2922  cm-1 and bending frequency  1255  cm-1