returns = pd.Series(np.array([0.03, 0.01, 0.05, -0.01, -0.03]))
compsum(returns)0 0.030000
1 0.040300
2 0.092315
3 0.081392
4 0.048950
dtype: float64Stats
Statistical functions for portfolio analysis
compsum
compsum (returns)
Calculates cumulative compounded returns up to each day, for series of daily returns
comp
comp (returns)
Calculates total compounded return, for series of daily returns
returns = pd.Series(np.array([0.03, 0.01, 0.05, -0.01, -0.03]))
comp(returns)0.048950094500000096distribution
distribution (returns, compounded=True, prepare_returns=False)
Show the returns and outlier values based on IQR from a series of returns. Outliers are those more than 1.5 times the IQR from the Q1/Q3
expected_return
expected_return (returns, aggregate=None, compounded=True, prepare_returns=True)
Returns the expected geometric return for a given period by calculating the geometric holding period return
The expected geometric return is: \[ \left(\prod\limits_{i=1}^{n}(p_{i})\right)^{(1/n)} -1\]
where \(p_{i}\) is 1+ the daily return: \(p_{i}=\frac{v_{i}}{v_{i-1}}=1+r_{i}\), where \(v_{i}\) and \(r_{i}\) are value and return of the asset on day \(i\) respectively
returns = pd.Series(np.array([0.03, 0.01, 0.05, -0.01, -0.03]))
expected_return(returns, aggregate=None, compounded=True,
prepare_returns=True)0.009603773872040255ghpr
ghpr (retruns, aggregate=None, compounded=True)
Shorthand for expected_return()
geometric_mean
geometric_mean (retruns, aggregate=None, compounded=True)
Shorthand for expected_return()
outliers
outliers (returns, quantile=0.95)
Returns series of outliers: all values greater than the quantile
returns = pd.Series(np.arange(1, 101, 1))
outliers(returns, quantile=.95)95 96
96 97
97 98
98 99
99 100
dtype: int32remove_outliers
remove_outliers (returns, quantile=0.95)
Returns series of returns without the outliers on the top end
returns = pd.Series(np.arange(1, 101, 1))
remove_outliers(returns, quantile=.95).tail(10) # the range goes from [1,100] to [1,95]85 86
86 87
87 88
88 89
89 90
90 91
91 92
92 93
93 94
94 95
dtype: int32best
best (returns, aggregate=None, compounded=True, prepare_returns=False)
Returns the best day/month/week/quarter/year’s return
returns = _utils.download_returns('SPY', '5y')
best(returns)
#best(returns)0.09060315805687602worst
worst (returns, aggregate=None, compounded=True, prepare_returns=False)
Returns the worst day/month/week/quarter/year’s return
returns = _utils.download_returns('SPY', '5y')
worst(returns)
#best(returns)-0.10942352331745997consecutive_wins
consecutive_wins (returns, aggregate=None, compounded=True, prepare_returns=False)
Returns the maximum consecutive wins by day/month/week/quarter/year
returns = _utils.download_returns('SPY', '5y')
consecutive_wins(returns)
#best(returns)11consecutive_losses
consecutive_losses (returns, aggregate=None, compounded=True, prepare_returns=False)
Returns the maximum consecutive losses by day/month/week/quarter/year
returns = _utils.download_returns('SPY', '5y')
consecutive_losses(returns)
#best(returns)8exposure
exposure (returns, prepare_returns=False)
Returns the market exposure time (returns != 0)
returns = _utils.download_returns('SPY', '5y')
exposure(returns)1.0win_rate
win_rate (returns, aggregate=None, compounded=True, prepare_returns=False)
Calculates the win ratio for a period: (number of winning days)/(number of days in market)
returns = _utils.download_returns('SPY', '5y')
win_rate(returns)0.5542264752791068avg_return
avg_return (returns, aggregate=None, compounded=True, prepare_returns=False)
Calculates the average return/trade return for a period
returns = _utils.download_returns('SPY', '5y')
avg_return(returns)0.0004451419089322777avg_win
avg_win (returns, aggregate=None, compounded=True, prepare_returns=False)
Calculates the average winning return/trade return for a period
returns = _utils.download_returns('SPY', '5y')
avg_win(returns)0.008044224938256789avg_loss
avg_loss (returns, aggregate=None, compounded=True, prepare_returns=False)
Calculates the average low if return/trade return for a period
returns = _utils.download_returns('SPY', '5y')
avg_loss(returns)-0.009002736188760357volatility
volatility (returns, periods=252, annualize=True, prepare_returns=False)
Calculates the volatility of returns for a period
Calculate volatility as \(\text{vol.}=\sigma\sqrt{T}\) where \(\sigma\) is the standard deviations of returns and \(T\) the number of periods in the time horizon
returns = _utils.download_returns('SPY', '5y')
volatility(returns)0.20844063908238844rolling_volatility
rolling_volatility (returns, rolling_period=126, periods_per_year=252, prepare_returns=False)
Create time series of rolling volatility
returns = _utils.download_returns('SPY', '1y')
rolling_volatility(returns).tail(10)Date
2022-09-16 0.248680
2022-09-19 0.248414
2022-09-20 0.248865
2022-09-21 0.249286
2022-09-22 0.248944
2022-09-23 0.248828
2022-09-26 0.248951
2022-09-27 0.248649
2022-09-28 0.249690
2022-09-29 0.251102
Name: Close, dtype: float64implied_volatility
implied_volatility (returns, periods=252, annualize=False)
Calculates the implied volatility of returns for a period
Implied volatility is defined here as the standard deviation of the log returns. This works under the assumption that returns are lognormally distributed and so the log of returns is a normal distribution.
returns = _utils.download_returns('SPY', '1y')
implied_volatility(returns)0.013801893088772903autocorr_penalty
autocorr_penalty (returns, prepare_returns=False)
Metric to account for auto correlation
returns = _utils.download_returns('SPY', '5y')
autocorr_penalty(returns)1.1893156409496177smart_sharpe
smart_sharpe (returns, rf=0.0, periods=252, annualize=True)
Sharpe ratio, penalised with autocorrelation penalty
returns = _utils.download_returns('SPY', '5y')
smart_sharpe(returns)0.4510622023704182rolling_sharpe
rolling_sharpe (returns, rf=0.0, rolling_period=126, annualize=True, periods_per_year=252, prepare_returns=False)
Calculate rolling Sharpe ratio over a period
returns = _utils.download_returns('SPY', '5y')
rolling_sharpe(returns).tail(10)Date
2022-09-16 -0.864632
2022-09-19 -0.891301
2022-09-20 -0.979586
2022-09-21 -1.211758
2022-09-22 -1.177445
2022-09-23 -1.433826
2022-09-26 -1.551825
2022-09-27 -1.631454
2022-09-28 -1.566138
2022-09-29 -1.674526
Name: Close, dtype: float64sortino
sortino (returns, rf=0, periods=252, annualize=True, smart=False, prepare_returns=False)
Calculates the sortino ratio of access returns If rf is non-zero, you must specify periods. In this case, rf is assumed to be expressed in yearly (annualized) terms Calculation is based on this paper by Red Rock Capital http://www.redrockcapital.com/Sortino__A__Sharper__Ratio_Red_Rock_Capital.pdf
Calculates Sortino ratio as \(\frac{\text{Expected Excess Return}}{\text{Downside Deviation}}\) where for \(n\) periods the Downside deviation is \(\sqrt{\frac{\sum d^{2}}{n}}\) where \(d\) is an excess return less than 0, and the expected excess return is the mean excess return, and annualised
returns = _utils.download_returns('SPY', '5y')
sortino(returns)0.7310777239511432smart_sortino
smart_sortino (returns, rf=0, periods=252, annualize=True)
Calculates Smart Sortino ratio, adding an autocorrelation penalty
returns = _utils.download_returns('SPY', '5y')
smart_sortino(returns)0.6147043287347095def adjusted_sortino(returns, rf=0, periods=252, annualize=True, smart=False):
"""
Jack Schwager's version of the Sortino ratio allows for
direct comparisons to the Sharpe. See here for more info:
https://archive.is/wip/2rwFW
"""
data = sortino(
returns, rf, periods=periods, annualize=annualize, smart=smart)
return data / sqrt(2)The adjusted sortino is defined as \(\text{Adj. Sortino}=\text{Sortino}/\sqrt{2}\)
returns = _utils.download_returns('SPY', '5y')
adjusted_sortino(returns)0.5169498730432484rolling_sortino
rolling_sortino (returns, rf=0, rolling_period=126, annualize=True, periods_per_year=252, **kwargs)
returns = _utils.download_returns('SPY', '5y')
rolling_sortino(returns).tail(10)Date
2022-09-16 -1.119173
2022-09-19 -1.152463
2022-09-20 -1.264410
2022-09-21 -1.554069
2022-09-22 -1.511805
2022-09-23 -1.826545
2022-09-26 -1.972788
2022-09-27 -2.071153
2022-09-28 -1.996554
2022-09-29 -2.124861
Name: Close, dtype: float64skew
skew (returns, prepare_returns=False)
Calculates returns’ skewness (the degree of asymmetry of a distribution around its mean)
The skew is defined as \(\text{Skew}(X)=\frac{E[(X-\mu)^{3}]}{E[(X-\mu)^{2}]^{3/2}}=\frac{\mu_{3}}{\sigma^{3}}\), where \(\mu\) is mean, \(\sigma\) stadard deviation and \(\mu_{3}\), third moment of inertia.
returns = _utils.download_returns('SPY', '5y')
skew(returns)-0.6567130752131589kurtosis
kurtosis (returns, prepare_returns=False)
Calculates returns’ kurtosis (the degree to which a distribution peak compared to a normal distribution)
The kurtosis is defined as \(\text{Kurt}(X)=\frac{E[(X-\mu)^{4}]}{E[(X-\mu)^{2}]^{2}}=\frac{\mu_{4}}{\sigma^{2}}\), where \(\mu\) is mean, \(\sigma\) stadard deviation and \(\mu_{4}\), fourth moment of inertia. A measure of ‘tailed’: higher kurtosis means fatter tails.
returns = _utils.download_returns('SPY', '5y')
kurtosis(returns)11.996182480024226<AxesSubplot:ylabel='Frequency'>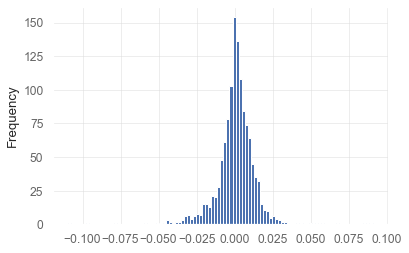
probabilistic_ratio
probabilistic_ratio (series, rf=0.0, base='sharpe', periods=252, annualize=False, smart=False)
probabilistic_sharpe_ratio
probabilistic_sharpe_ratio (series, rf=0.0, periods=252, annualize=False, smart=False)
The probabilistic Sharpe Ratio
returns = _utils.download_returns('SPY', '5y')
probabilistic_sharpe_ratio(returns)0.8816407449051655probabilistic_sortino_ratio
probabilistic_sortino_ratio (series, rf=0.0, periods=252, annualize=False, smart=False)
The probabilistic Sortino Ratio
returns = _utils.download_returns('SPY', '5y')
probabilistic_sortino_ratio(returns)0.9456555568118186probabilistic_adjusted_sortino_ratio
probabilistic_adjusted_sortino_ratio (series, rf=0.0, periods=252, annualize=False, smart=False)
The probabilistic adj. Sortino Ratio
returns = _utils.download_returns('SPY', '5y')
probabilistic_adjusted_sortino_ratio(returns)0.8730193107071486omega
omega (returns, rf=0.0, required_return=0.0, periods=252, **kwargs)
Determines the Omega ratio of a strategy. See https://en.wikipedia.org/wiki/Omega_ratio for more details.
This is broken
returns = _utils.download_returns('SPY', '5y')
#omega(returns, 0.01)gain_to_pain_ratio
gain_to_pain_ratio (returns, rf=0, resolution='D', **kwargs)
Jack Schwager’s GPR. See here for more info: https://archive.is/wip/2rwFW
This seems to be wrong
returns = _utils.download_returns('SPY', '5y')
gain_to_pain_ratio(returns, 10)0.11091999229680034cagr
cagr (returns, rf=0.0, compounded=True, **kwargs)
Calculates the communicative annualized growth return (CAGR%) of access returns If rf is non-zero, you must specify periods?. In this case, rf is assumed to be expressed in yearly (annualized) terms
Check
returns = _utils.download_returns('SPY', '5y')
cagr(returns, 10)0.09407550605477089rar
rar (returns, rf=0.0, **kwargs)
Calculates the risk-adjusted return of access returns (CAGR / exposure. takes time into account.) If rf is non-zero, you must specify periods. In this case, rf is assumed to be expressed in yearly (annualized) terms
Check if this should be excess return
returns = _utils.download_returns('SPY', '5y')
rar(returns)0.09407549161897544max_drawdown
max_drawdown (returns)
Calculates the maximum drawdown
returns = _utils.download_returns('SPY', '5y')
max_drawdown(returns)-0.3371726193896011to_drawdown_series
to_drawdown_series (returns)
Convert returns series to drawdown series
returns = _utils.download_returns('SPY', '5y')
to_drawdown_series(returns).tail(10)Date
2022-09-16 -0.183555
2022-09-19 -0.177223
2022-09-20 -0.186668
2022-09-21 -0.200855
2022-09-22 -0.207568
2022-09-23 -0.220845
2022-09-26 -0.228553
2022-09-27 -0.230522
2022-09-28 -0.215382
2022-09-29 -0.231771
Name: Close, dtype: float64calmar
calmar (returns, prepare_returns=False)
Calculates the calmar ratio (CAGR% / MaxDD%)
returns = _utils.download_returns('SPY', '5y')
calmar(returns)0.27901279782780064ulcer_index
ulcer_index (returns)
Calculates the ulcer index score (downside risk measurment)
Define properly
returns = _utils.download_returns('SPY', '5y')
ulcer_index(returns)0.07637641267955013ulcer_performance_index
ulcer_performance_index (returns, rf=0)
Calculates the ulcer index score (downside risk measurment)
returns = _utils.download_returns('SPY', '5y')
ulcer_performance_index(returns)7.4215621009669315upi
upi (returns, rf=0)
Shorthand for ulcer_performance_index()
risk_of_ruin
risk_of_ruin (returns, prepare_returns=False)
Calculates the risk of ruin (the likelihood of losing all one’s investment capital)
Check definition
returns = _utils.download_returns('SPY', '5y')
risk_of_ruin(returns)0.0ror
ror (returns)
Shorthand for risk_of_ruin()
value_at_risk
value_at_risk (returns, sigma=1, confidence=0.95, prepare_returns=False)
Calculats the daily value-at-risk (variance-covariance calculation with confidence n)
Define
returns = _utils.download_returns('SPY', '5y')
value_at_risk(returns)-0.021154066958981442var
var (returns, sigma=1, confidence=0.95, prepare_returns=False)
Shorthand for value_at_risk()
conditional_value_at_risk
conditional_value_at_risk (returns, sigma=1, confidence=0.95, prepare_returns=False)
Calculats the conditional daily value-at-risk (aka expected shortfall) quantifies the amount of tail risk an investment
returns = _utils.download_returns('SPY', '5y')
conditional_value_at_risk(returns)-0.03378474064120063cvar
cvar (returns, sigma=1, confidence=0.95, prepare_returns=False)
Shorthand for conditional_value_at_risk()
expected_shortfall
expected_shortfall (returns, sigma=1, confidence=0.95, prepare_returns=False)
Shorthand for conditional_value_at_risk()
serenity_index
serenity_index (returns, rf=0)
Calculates the serenity index score (https://www.keyquant.com/Download/GetFile?Filename=%5CPublications%5CKeyQuant_WhitePaper_APT_Part1.pdf)
returns = _utils.download_returns('SPY', '5y')
serenity_index(returns)0.5104927720686929tail_ratio
tail_ratio (returns, cutoff=0.95, prepare_returns=False)
Measures the ratio between the right (95%) and left tail (5%).
returns = _utils.download_returns('SPY', '5y')
tail_ratio(returns)0.8246500295451326payoff_ratio
payoff_ratio (returns, prepare_returns=False)
Measures the payoff ratio (average win/average loss)
Should probably rate this by win rate/loss rate
returns = _utils.download_returns('SPY', '5y')
payoff_ratio(returns)0.8935312962081646win_loss_ratio
win_loss_ratio (returns, prepare_returns=False)
Shorthand for payoff_ratio()
profit_ratio
profit_ratio (returns, prepare_returns=False)
Measures the profit ratio (win ratio / loss ratio)
returns = _utils.download_returns('SPY', '5y')
profit_ratio(returns)0.7104803267194572profit_factor
profit_factor (returns, prepare_returns=False)
Measures the profit ratio (wins/loss)
returns = _utils.download_returns('SPY', '5y')
profit_factor(returns)1.1109199478795606cpc_index
cpc_index (returns, prepare_returns=False)
Measures the cpc ratio (profit factor * win % * win loss ratio)
returns = _utils.download_returns('SPY', '5y')
profit_factor(returns)1.1109200029518147common_sense_ratio
common_sense_ratio (returns, prepare_returns=False)
Measures the common sense ratio (profit factor * tail ratio)
returns = _utils.download_returns('SPY', '5y')
common_sense_ratio(returns)0.9161143659778377outlier_win_ratio
outlier_win_ratio (returns, quantile=0.99, prepare_returns=False)
Calculates the outlier winners ratio 99th percentile of returns / mean positive return
returns = _utils.download_returns('SPY', '5y')
outlier_win_ratio(returns)3.8800605330519113outlier_loss_ratio
outlier_loss_ratio (returns, quantile=0.01, prepare_returns=False)
Calculates the outlier losers ratio 1st percentile of returns / mean negative return
returns = _utils.download_returns('SPY', '5y')
outlier_loss_ratio(returns)4.188328392594448recovery_factor
recovery_factor (returns, prepare_returns=False)
Measures how fast the strategy recovers from drawdowns
returns = _utils.download_returns('SPY', '5y')
recovery_factor(returns)1.6811327076863491risk_return_ratio
risk_return_ratio (returns, prepare_returns=True)
Calculates the return / risk ratio (sharpe ratio without factoring in the risk-free rate)
returns = _utils.download_returns('SPY', '5y')
risk_return_ratio(returns)0.033793529561903915drawdown_details
drawdown_details (drawdown)
Calculates drawdown details, including start/end/valley dates, duration, max drawdown and max dd for 99% of the dd period for every drawdown period
returns = _utils.download_returns('SPY', '5y')
drawdown = to_drawdown_series(returns)
drawdown_details(drawdown).tail(10)| start | valley | end | days | max drawdown | 99% max drawdown | |
|---|---|---|---|---|---|---|
| 86 | 2021-09-03 | 2021-10-04 | 2021-10-20 | 47 | -5.114137 | -5.003459 |
| 87 | 2021-10-22 | 2021-10-22 | 2021-10-25 | 3 | -0.103615 | 0.000000 |
| 88 | 2021-10-27 | 2021-10-27 | 2021-10-28 | 1 | -0.443010 | 0.000000 |
| 89 | 2021-11-09 | 2021-11-10 | 2021-11-16 | 7 | -1.132363 | -1.100381 |
| 90 | 2021-11-17 | 2021-11-17 | 2021-11-18 | 1 | -0.242927 | 0.000000 |
| 91 | 2021-11-19 | 2021-12-01 | 2021-12-10 | 21 | -4.093850 | -3.472205 |
| 92 | 2021-12-13 | 2021-12-20 | 2021-12-23 | 10 | -3.008357 | -1.965921 |
| 93 | 2021-12-28 | 2021-12-28 | 2021-12-29 | 1 | -0.081728 | 0.000000 |
| 94 | 2021-12-30 | 2021-12-31 | 2022-01-03 | 4 | -0.527776 | -0.276447 |
| 95 | 2022-01-04 | 2022-09-29 | 2022-09-29 | 268 | -23.177148 | -23.009976 |
kelly_criterion
kelly_criterion (returns, prepare_returns=False)
Calculates the recommended maximum amount of capital that should be allocated to the given strategy, based on the Kelly Criterion (http://en.wikipedia.org/wiki/Kelly_criterion)
returns = _utils.download_returns('SPY', '5y')
kelly_criterion(returns)0.05533682629177291Comparing against a benchmark
r_squared
r_squared (returns, benchmark, prepare_returns=True)
Measures the straight line fit of the equity curve
SPY = _utils.download_prices('SPY', '5y')
r_squared(SPY, 'QQQ')0.8657597594693889r2
r2 (returns, benchmark)
Shorthand for r_squared()
information_ratio
information_ratio (returns, benchmark, prepare_returns=True)
Calculates the information ratio (basically the risk return ratio of the net profits)
SPY = _utils.download_prices('SPY', '5y')
information_ratio(SPY, 'QQQ')-0.034145732893584566greeks
greeks (returns, benchmark, periods=252.0, prepare_returns=True)
Calculates alpha and beta of the portfolio
SPY = _utils.download_prices('SPY', '5y')
greeks(SPY, 'QQQ')beta 0.766525
alpha -0.014009
dtype: float64rolling_greeks
rolling_greeks (returns, benchmark, periods=252, prepare_returns=True)
Calculates rolling alpha and beta of the portfolio
SPY = _utils.download_prices('SPY', '5y')
rolling_greeks(SPY, 'QQQ').tail(10)| beta | alpha | |
|---|---|---|
| Date | ||
| 2022-09-16 | 0.711193 | -0.000020 |
| 2022-09-19 | 0.711200 | -0.000020 |
| 2022-09-20 | 0.711199 | -0.000020 |
| 2022-09-21 | 0.712228 | -0.000020 |
| 2022-09-22 | 0.711855 | -0.000020 |
| 2022-09-23 | 0.712161 | -0.000020 |
| 2022-09-26 | 0.712399 | -0.000020 |
| 2022-09-27 | 0.712574 | -0.000020 |
| 2022-09-28 | 0.713869 | -0.000021 |
| 2022-09-29 | 0.714026 | -0.000021 |
treynor_ratio
treynor_ratio (returns, benchmark, periods=252.0, rf=0.0, prepare_returns=True)
Calculates the Treynor ratio Args: * returns (Series, DataFrame): Input return series * benchmatk (String, Series, DataFrame): Benchmark to compare beta to * periods (int): Freq. of returns (252/365 for daily, 12 for monthly)
SPY = _utils.download_prices('SPY', '5y')
treynor_ratio(SPY, 'QQQ')0.7394830437816903compare
compare (returns, benchmark, aggregate=None, compounded=True, round_vals=None, prepare_returns=True)
Compare returns to benchmark on a day/week/month/quarter/year basis
SPY = _utils.download_returns('SPY', '5y')
compare(SPY, 'QQQ', aggregate = 'M').tail(12)| Returns | Benchmark | Multiplier | Won | |
|---|---|---|---|---|
| (2021, 10) | 7.016350 | 7.864013 | 0.892210 | - |
| (2021, 11) | -0.803480 | 1.996842 | -0.402376 | - |
| (2021, 12) | 4.624778 | 1.152342 | 4.013372 | + |
| (2022, 1) | -5.274126 | -8.747021 | 0.602963 | + |
| (2022, 2) | -2.951699 | -4.475968 | 0.659455 | + |
| (2022, 3) | 3.759043 | 4.667878 | 0.805300 | - |
| (2022, 4) | -8.776911 | -13.595739 | 0.645563 | + |
| (2022, 5) | 0.225728 | -1.586593 | -0.142272 | + |
| (2022, 6) | -8.246043 | -8.907885 | 0.925702 | + |
| (2022, 7) | 9.208745 | 12.551730 | 0.733663 | - |
| (2022, 8) | -4.080199 | -5.132186 | 0.795022 | + |
| (2022, 9) | -7.819145 | -8.992359 | 0.869532 | + |
Note that these returns are already formatted in percentage terms
monthly_returns
monthly_returns (returns, eoy=True, compounded=True, prepare_returns=True)
Calculates monthly returns
SPY = _utils.download_prices('SPY', '5Y')
monthly_returns(SPY)| JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC | EOY | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2017 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.019142 | 0.030566 | 0.012128 | 0.063031 |
| 2018 | 0.056359 | -0.036360 | -0.027411 | 0.005168 | 0.024309 | 0.005751 | 0.037047 | 0.031920 | 0.005945 | -0.069104 | 0.018549 | -0.088049 | -0.045690 |
| 2019 | 0.080066 | 0.032416 | 0.018100 | 0.040852 | -0.063771 | 0.069586 | 0.015119 | -0.016743 | 0.019458 | 0.022105 | 0.036198 | 0.029055 | 0.312239 |
| 2020 | -0.000404 | -0.079166 | -0.124871 | 0.126983 | 0.047645 | 0.017735 | 0.058892 | 0.069797 | -0.037444 | -0.024933 | 0.108777 | 0.037049 | 0.183316 |
| 2021 | -0.010191 | 0.027805 | 0.045399 | 0.052911 | 0.006566 | 0.022427 | 0.024413 | 0.029760 | -0.046605 | 0.070163 | -0.008035 | 0.046248 | 0.287287 |
| 2022 | -0.052741 | -0.029517 | 0.037590 | -0.087769 | 0.002257 | -0.082460 | 0.092087 | -0.040802 | -0.078191 | 0.000000 | 0.000000 | 0.000000 | -0.227324 |